Trong hình học tập, cát tuyến là 1 trong định nghĩa cần thiết và thông thường xuất hiện nay trong số Việc về lối tròn trĩnh. Vậy cát tuyến là gì? Cát tuyến của lối tròn trĩnh đem đặc điểm và được xác lập như vậy nào? Bài ghi chép tiếp sau đây cũng trình làng một trong những Việc tương quan cho tới cát tuyến của lối tròn trĩnh.
1. Khái niệm và phần mềm của cát tuyến:
1.1. Khái niệm của cát tuyến:
Cát tuyến là 1 trong kể từ Hán Việt với “cát” tức là tách, “tuyến” là đường thẳng liền mạch, cát tuyến là đường thẳng liền mạch cắt theo đường ngang qua quýt một mặt phẳng khác ví như lối cong, lối tròn trĩnh,… Định nghĩa cát tuyến của lối tròn trĩnh được nêu vô sách giáo khoa hình học tập lớp 9 như sau:
Cát tuyến của lối tròn trĩnh đó là đường thẳng liền mạch tách lối tròn trĩnh bại liệt bên trên 2 điểm phân biệt. Tức là uỷ thác điểm đằm thắm lối cát tuyến và lối tròn trĩnh là nhị điểm nằm trong lối tròn trĩnh bại liệt. Trường ăn ý đặc trưng của cát tuyến đó là đường thẳng liền mạch trải qua tâm của lối tròn trĩnh. Khi ấy cát tuyến của lối tròn trĩnh tiếp tục trùng với 2 lần bán kính lối tròn trĩnh bại liệt.
Một số ví dụ về lối cát tuyến:
Vd1: Cát tuyến của hai tuyến phố trực tiếp là 1 trong đường thẳng liền mạch tách hai tuyến phố trực tiếp bại liệt.
Vd2: Cát tuyến của lối tròn trĩnh tách lối tròn trĩnh bên trên nhị điểm bất kì nằm trong lối tròn trĩnh bại liệt.
Vd3: cát tuyến của một cung tròn trĩnh tách cung tròn trĩnh bên trên nhị điểm phân biệt.
1.2. Ứng dụng lối cát tuyến hình tròn:
Đường cát tuyến hình trụ rất có thể được dùng nhằm giải những Việc tương quan cho tới tỉ lệ thành phần, tam giác đồng dạng, lối tròn trĩnh nội tiếp và nước ngoài tiếp. Một số ví dụ về phần mềm lối cát tuyến hình trụ là:
- Tính độ cao của một ngọn núi lúc biết tầm nhìn kể từ nhị điểm xa nhau chừng một khoảng tầm xác lập.
- Tính nửa đường kính của một lối tròn trĩnh lúc biết nhị cát tuyến của chính nó và khoảng cách đằm thắm nhị nút giao của bọn chúng với lối tròn trĩnh.
- Tính diện tích S của một tứ giác nội tiếp vô một lối tròn trĩnh lúc biết những cạnh của chính nó và những góc tạo nên vày những cát tuyến của bọn chúng.
- Tính chiều lâu năm của một cung tròn trĩnh lúc biết nhị tiếp tuyến và một cát tuyến của nó
Đường cát tuyến là đường thẳng liền mạch tách một lối không giống (đường trực tiếp, lối tròn trĩnh, lối cong,…) bên trên nhị điểm phân biệt. Đường cát tuyến đem một trong những đặc điểm sau:
- Nếu hai tuyến phố trực tiếp chứa chấp những thừng của một lối tròn trĩnh tách nhau bên trên một điểm thì tích những đoạn của từng thừng cân nhau.
- Nếu hai tuyến phố trực tiếp tách nhau bên trên một điểm và tích những đoạn của từng lối cân nhau thì tứ điểm nằm trong và một lối tròn trĩnh.
- Nếu một đường thẳng liền mạch là tiếp tuyến và một đường thẳng liền mạch là cát tuyến của một lối tròn trĩnh thì bình phương của tiếp tuyến vày tích nhị đoạn của cát tuyến.
- Nếu từ là một điểm ngoài lối tròn trĩnh kẻ nhị tiếp tuyến và một cát tuyến thì trung điểm của cát tuyến nằm trong trung trực của nhị tiếp điểm.
- Nếu từ là một điểm ngoài lối tròn trĩnh kẻ nhị tiếp tuyến và một cát tuyến thì tỉ số những đoạn của cát tuyến vày tỉ số những tiếp tuyến
3. Cách xác lập cát tuyến phố tròn:
Cách vẽ lối cát tuyến của lối tròn trĩnh và lối cong là đòi hỏi cơ bạn dạng vô Việc tương quan cho tới lối cát tuyến. Sau phía trên công ty chúng tôi tiếp tục chỉ dẫn các bạn phương pháp vẽ cát tuyến chỉ với 2 bước giản dị là:
- Bước 1: Xác ấn định nhị điểm bất kì nằm trong lối tròn trĩnh hoặc cung tròn trĩnh. Lưu ý so với lối tròn trĩnh, nếu như không tồn tại đòi hỏi đặc trưng thì các bạn ko nên lựa chọn nhị điểm phía trên 2 lần bán kính của lối tròn trĩnh bại liệt.
- Bước 2: Vẽ một đường thẳng liền mạch bằng phương pháp nối nhị điểm vừa vặn xác lập. Đường trực tiếp này đó là lối cát tuyến, nó tách và phân chia lối tròn trĩnh trở thành nhị cung.
Ngoài đi ra, các bạn cũng rất có thể người sử dụng những đặc điểm của cát tuyến nhằm xác lập cát tuyến của lối tròn trĩnh. Một số đặc điểm cần thiết là: Nếu hai tuyến phố trực tiếp chứa chấp những thừng của một lối tròn trĩnh tách nhau bên trên một điểm thì tích những đoạn của từng thừng cân nhau. Nếu một đường thẳng liền mạch là tiếp tuyến và một đường thẳng liền mạch là cát tuyến của một lối tròn trĩnh thì bình phương của tiếp tuyến vày tích nhị đoạn của cát tuyến. Nếu từ là một điểm ngoài lối tròn trĩnh kẻ nhị tiếp tuyến và một cát tuyến thì tỉ số những đoạn của cát tuyến vày tỷ số những tiếp tuyến.
4. Bài tập luyện về cát tuyến:
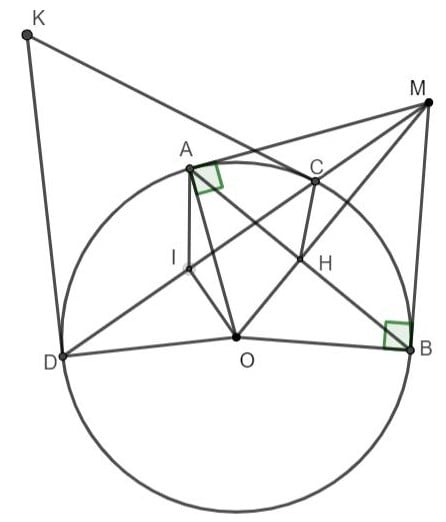
Ví dụ 1: Từ một điểm M ở ngoài lối tròn trĩnh (O) các bạn hãy vẽ 1 lối cát tuyến MCD ko trải qua tâm lối tròn trĩnh O và đem nhị tiếp tuyến theo thứ tự là MA và MB cho tới lối tròn trĩnh (O). Tại phía trên A, B đó là những tiếp điểm và điểm C tiếp tục nằm trong lòng M, D.
1. Chứng minh bất đẳng thức sau : MA.MA = MC.MD
2. Gọi I đó là trung điểm của đoạn trực tiếp CD. Hãy chứng tỏ rằng 4 điểm M, A, O, I, B nằm trong phía trên 1 lối tròn trĩnh.
3. Gọi H là uỷ thác điểm của hai tuyến phố trực tiếp HB và MO. Hãy chứng tỏ rằng tứ giác CHOD là tứ giác nội tiếp với lối tròn trĩnh (O) và HB là lối phân giác của góc CHD.
4. Gọi K là uỷ thác điểm của những tiếp tuyến theo thứ tự bên trên nhị điểm C và D của lối tròn trĩnh (O). Hãy chứng tỏ rằng 3 điểm A, B, K tiếp tục nằm trong phía trên một đường thẳng liền mạch.
Gợi ý đáp án:
Vì MA đó là tiếp tuyến của lối tròn trĩnh (O) nên tao có:
Góc MAC vày Góc MDA suy đi ra ΔMAC ~ ΔMDA (g.g)
=> MA/MD tiếp tục vày MC/MA suy đi ra MA.MA vày MC.MD
Vì I là trung điểm của CD nên suy ra
Góc MIO = 90 phỏng và vày với góc MAO và góc MBO. Từ những điểm bên trên tao rất có thể tóm lại được M, A, O, I, B tiếp tục nằm trong tuỳ thuộc bên trên 1 lối tròn trĩnh.
Vì tao đem đoạn MA vuông góc với đoạn OA, đoạn OM vuông góc với đoạn OB bên trên điểm H. Suy đi ra MH.MO vày MA.MA vày MC.MD
=> MA/MD vày MC/MA -> ΔMHC ~ ΔMDC -> Góc MHC vày với góc MDO.
=> Tứ giác HDCO là tứ giác nội tiếp của lối tròn trĩnh tâm O.
=> Góc OHD vày góc OCD vày góc ODC vày góc MHC
Ta đem 90 phỏng – góc MHC = 90 phỏng – góc OHD sau đi ra góc CHB vày với góc BHD
Từ bại liệt tao rất có thể tóm lại rằng: đoạn HB đó là phân giác của góc CHD.
Ta đem HB là phân giác của góc CHD
Vì KC, KD theo thứ tự là hai tuyến phố tiếp tuyến của lối tròn trĩnh (O) suy đi ra KCOD là tứ giác nội tiếp lối tròn trĩnh (O) nhưng mà HOCD lại là tứ giác nội tiếp (chứng minh trên). Như vậy suy đi ra 4 điểm K, C, H, O, D nên nằm trong phía trên 1 lối tròn trĩnh.
Mà lại sở hữu HK là phân giác của góc CHD vì thế KC tiếp tục vày KD
=> 3 điểm A, B, K nên trực tiếp mặt hàng.
Ví dụ 2: Cho 2 đường thẳng liền mạch tuy vậy song a, b và một lối cát tuyến c. Hai tia phân giác của cặp góc vô nằm trong phía tách nhau bên trên điểm I. Chứng minh điểm I cơ hội đều 3 đường thẳng liền mạch a, b và c.

Gợi ý đáp án:
Gọi 3 điểm A, B, C theo thứ tự là chân lối vuông góc kẻ kể từ điểm I cho tới a, b, c.
Xét nhị góc vô nằm trong phía CEA và CFB tao có:
Do I phía trên tia phân giác của góc CEA nên IA = IC (1)
Do I phía trên tia phân giác của góc CFB nên IC = IB (2)
Từ (1) và (2) => IA = IB = IC
=> I cơ hội đều đường thẳng liền mạch a, b và c.
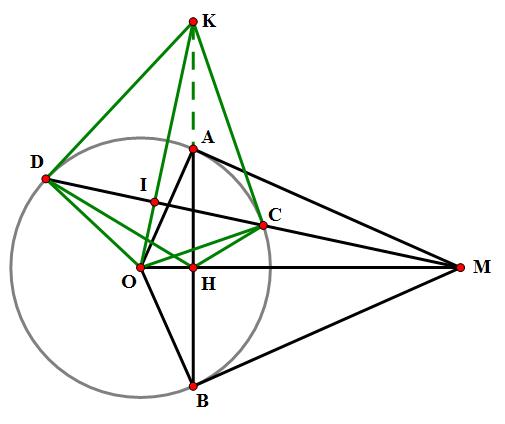
Ví dụ 3: Từ điểm K ở bên phía ngoài lối tròn trĩnh tâm O, hãy kẻ những tiếp tuyến KA, KB và kẻ thêm thắt lối cát tuyến KCD cho tới lối tròn trĩnh. Lấy M là uỷ thác điểm AB và OK. Vẽ đoạn DI trải qua M. Chứng minh:
a) KIOD là tứ giác nội tiếp.
b) KO là lối phân giác góc IKD.
Gợi ý đáp án:
a)
Ta đem tứ giác AIBD nội tiếp lối tròn trĩnh (O) và AB ⋂ ID = M
=> MA.MB = XiaoMi MI.MD (1)
Mặt không giống tao đem góc KAO = góc KBO = 900 => OBKA là tứ giác nội tiếp
=> MA.MB = MO.MK (2)
Từ (1) và (2) => XiaoMi MI.MD = MO.MK
=> KIOD là 1 trong tứ giác nội tiếp
b)
Vì KIOD là tứ giác nội tiếp
Nên góc DKO = góc DIO
góc OKI = góc ODI
Mà ΔDOI cân nặng bên trên O nên góc DIO = góc DOI
=> góc DKO = góc OKI
Do bại liệt KO là phân giác góc IKD