Tam giác đều là một trong những hình học tập cơ phiên bản vô toán học tập và được phần mềm trong vô số nghành nghề dịch vụ không giống nhau. Việc tính diện tích S tam giác đều hùn hiểu thâm thúy rộng lớn về đặc thù hình học tập và ý nghĩa cần thiết vô thực dẫn. Trong nội dung bài viết này của FPT Shop, tất cả chúng ta tiếp tục tò mò cụ thể về tam giác đều, phương pháp tính diện tích S tam giác đều và những phần mềm thực tiễn của công thức này.
Tam giác đều là gì?
Tam giác đều là một trong những tam giác sở hữu những góc đều bằng nhau (60 độ) và những cạch cũng đều bằng nhau. Đây là loại tam giác quan trọng với tính đối xứng hoàn hảo nhất. Mỗi đỉnh của tam giác đều cơ hội đều những đỉnh còn sót lại và phân tách mặt mũi bằng phẳng trở nên tía phần đều bằng nhau. Vì tính đối xứng và giản dị, tam giác đều thông thường xuất hiện nay trong vô số vấn đề hình học tập cơ phiên bản và phần mềm thực dẫn.

Cách tính diện tích S tam giác đều
Cách tính diện tích S tam giác đều tiếp tục phụ thuộc vào công thức tính diện tích S tam giác ngẫu nhiên.
Diện tích của một tam giác ngẫu nhiên được xem vì chưng công thức:
- S= một nửa x a x h.
Trong đó:
- S là diện tích S tam giác.
- a là chừng lâu năm cạnh lòng (cạnh tam giác).
- h là độ cao ứng với cạnh lòng.
Ví dụ: Tính diện tích S của tam giác đều sở hữu cạnh lâu năm 6 centimet và đàng cao 10 centimet.
- Độ lâu năm cạnh tam giác: a = 6 centimet.
- Đường cao của tam giác: h = 10 centimet.
Áp dụng công thức phương pháp tính diện tích S tam giác đều như sau:
- S= một nửa x 6 x 10 = 60/2 = 30 cm².
Vậy, diện tích S của tam giác đều sở hữu cạnh 6 centimet và đàng cao 10 centimet là 30 cm².
Trường phù hợp chỉ biết chiều lâu năm cạnh
Nếu các bạn chỉ biết chiều lâu năm cạnh của tam giác, bạn cũng có thể vẽ một đường thẳng liền mạch kể từ đỉnh tam giác cho tới trung điểm của cạnh lòng sẽ tạo trở nên đàng cao. Đường cao này tiếp tục phân tách cạnh lòng trở nên nhì phần đều bằng nhau. Khi tê liệt, bạn cũng có thể dùng toan lý Pythagore
(a² + b² = c²) nhằm tính đàng cao, tiếp sau đó vận dụng công thức tính diện tích S tam giác đều như tiếp tục nêu trước tê liệt.Hoặc, nhằm giản dị và tiết kiệm chi phí thời hạn, bạn cũng có thể người sử dụng tức thì công thức tính nhanh:
- S= a² √3/4.
Điều này tức là các bạn lấy bình phương chiều lâu năm cạnh của tam giác đều, nhân với √3, rồi phân tách mang lại 4 nhằm tính diện tích S.
Ví dụ:
Tính diện tích S tam giác ABC sở hữu 3 cạnh đều bằng nhau, từng cạnh lâu năm 6 centimet.
Vì tam giác ABC sở hữu 3 cạnh đều bằng nhau, nên này đó là tam giác đều. kề dụng công thức bên trên, tớ sở hữu diện tích S tam giác ABC bằng:
- S= 6² √3/4 = 15.6 cm².
Trường phù hợp đề đòi hỏi tính đàng cao của tam giác đều
Ngoài việc tính diện tích S, đề bài bác cũng hoàn toàn có thể đòi hỏi các bạn tính đàng cao của tam giác đều. Trước Khi xử lý, bạn phải làm rõ đặc thù của đàng cao vô tam giác đều:
- Đường cao của tam giác đều là đoạn trực tiếp từ là một đỉnh của tam giác cho tới trung điểm của cạnh đối lập và vuông góc với cạnh tê liệt.
- Trong tam giác đều, tía đàng cao có tính lâu năm đều bằng nhau và gửi gắm nhau bên trên một điểm có một không hai - trọng tâm của tam giác. Điểm này cũng chính là gửi gắm điểm của những đàng phân giác, đàng trung trực và đàng trung tuyến.
- Để tính chiều lâu năm đàng cao của tam giác đều, bạn cũng có thể dùng công thức: đó là chừng lâu năm cạnh của tam giác đều.
Ví dụ:
Tính chiều lâu năm đàng cao AH của tam giác đều ABC, biết AB lâu năm 5 centimet.
Áp dụng công thức bên trên, tất cả chúng ta sở hữu thành phẩm như sau:
- AH = 5² √3/2 ≈ 4.33cm
Xem thêm: Cách tính diện tích S hình vuông vắn và chỉ dẫn thực hiện một số trong những dạng bài bác tập luyện thông thường bắt gặp nhất
Ứng dụng thực tiễn của việc tính diện tích S tam giác đều
Tính diện tích S tam giác đều không chỉ có là một trong những vấn đề toán học tập đơn thuần nhưng mà còn tồn tại phần mềm thực tiễn thoáng rộng trong vô số nghành nghề dịch vụ.
1. Trong phong cách thiết kế và thiết kế
Trong nhiều công trình xây dựng phong cách thiết kế, tam giác đều được dùng sẽ tạo rời khỏi những kết cấu vững chãi và sở hữu tính thẩm mỹ và làm đẹp cao. Việc đo lường và tính toán đúng mực diện tích S tam giác đều hùn những phong cách thiết kế sư phân loại không khí hiệu suất cao, nhất là trong những công việc kiến thiết những tòa căn nhà sở hữu cái vòm tam giác hoặc những phong cách thiết kế hình tam giác đều phức tạp.

2. Trong nghệ thuật và xây dựng
Công thức tính diện tích S tam giác đều còn vô cùng hữu ích vô nghành nghề dịch vụ nghệ thuật và kiến thiết. Khi kiến thiết những kết thông số kỹ thuật tam giác, như cái căn nhà hoặc giàn giáo, việc đo lường và tính toán diện tích S tam giác đều hùn đo lường và tính toán được lượng vật tư quan trọng mang lại tiến hành, tối ưu ngân sách, lực lượng lao động và thời hạn.

3. Thiết nối tiếp hình họa và thẩm mỹ sáng sủa tạo
Việc đo lường và tính toán diện tích S tam giác đều hùn những căn nhà kiến thiết bằng vận hình hình ảnh và không khí một cơ hội hợp lý, tạo thành những thành phầm kiến thiết tinh xảo và lạ mắt.
4. Trong giáo dục
Trong công tác học tập toán ở những ngôi trường học tập, việc tính diện tích S tam giác đều là một trong những phần cần thiết hùn học viên hiểu về hình học tập và những công thức toán học tập cơ phiên bản. Bài toán này hùn học viên cải cách và phát triển tài năng trí tuệ logic và xử lý yếu tố thực dẫn.
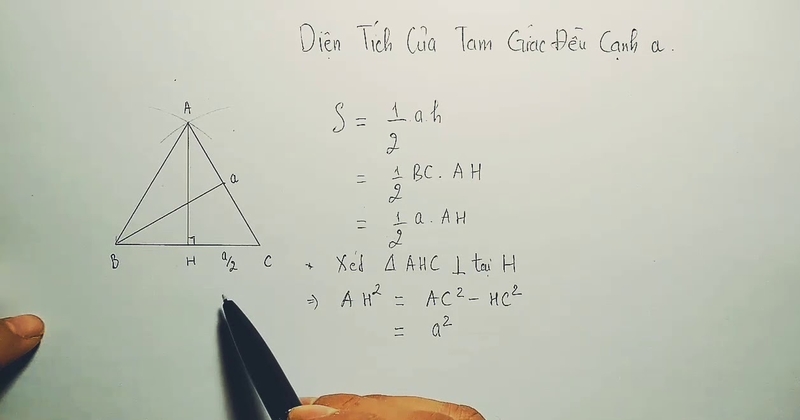
Những cảnh báo Khi tính diện tích S tam giác đều
Khi tính diện tích S tam giác đều, bạn phải cảnh báo một số trong những điểm sau nhằm đáp ứng thành phẩm chủ yếu xác:
- Đảm bảo trúng chừng lâu năm cạnh: Độ lâu năm cạnh là nhân tố cần thiết nhất vô công thức tính diện tích S tam giác đều. Hãy đảm nói rằng các bạn đo đúng mực chiều lâu năm của những cạnh trước lúc vận dụng công thức.
- Sử dụng trúng đơn vị chức năng đo lường: Khi tính diện tích S tam giác đều, đảm nói rằng những đơn vị chức năng đo của cạnh và thành phẩm diện tích S đều và một khối hệ thống đơn vị chức năng (cm, m, inch, v.v.).
- Áp dụng công thức trúng cách: Hãy đảm nói rằng các bạn làm rõ từng nhân tố vô công thức trước lúc triển khai phép tắc tính.

Tạm kết
Cách tính diện tích S tam giác đều là một trong những trong mỗi kỹ năng và kiến thức cơ phiên bản vô toán học tập tuy nhiên lại sở hữu nhiều phần mềm thực dẫn vô cuộc sống và việc làm. Từ việc kiến thiết phong cách thiết kế cho tới tối ưu hóa ngân sách vô kiến thiết, việc tính diện tích S tam giác đều hùn xử lý nhiều yếu tố cần thiết. Hy vọng qua chuyện nội dung bài viết này, các bạn tiếp tục làm rõ rộng lớn về phong thái tính diện tích S tam giác đều và những phần mềm thực tiễn của tam giác đều.
Hiện ni sở hữu thật nhiều phần mềm đo lường và tính toán bên trên Smartphone, khiến cho bạn triển khai những phép tắc tính kể từ cơ phiên bản cho tới phức tạp chỉ vô vài ba giây. Nếu các bạn đang được dò thám tìm tòi một cái điện thoại thông minh mạnh mẽ và uy lực, tương hỗ chất lượng tốt cho những nhu yếu tiếp thu kiến thức, thao tác làm việc và vui chơi, hãy cho tới tức thì FPT Shop nhé.
Mua tức thì iPhone bên trên FPT Shop nhằm nhận ưu đãi và chính sách BH uy tín:
- iPhone.
Xem thêm:
- Công thức tính diện tích S hình thang và 4 cảnh báo cần thiết Khi thực hiện những dạng bài bác tập luyện liên quan
- Khám phá huỷ công thức tính diện tích S hình chữ nhật thời gian nhanh gọn gàng và đúng mực nhất
