Hiểu rõ rệt công thức tính thể tích hình trụ tiếp tục khiến cho bạn xử lý nhiều câu hỏi thực tiễn biệt tương quan cho tới việc đo lường và tính toán và đo lường và tính toán không khí. Trong nội dung bài viết này, hãy nằm trong FPT Shop mò mẫm hiểu cụ thể công thức tính thể tích hình trụ.
Giới thiệu về hình trụ
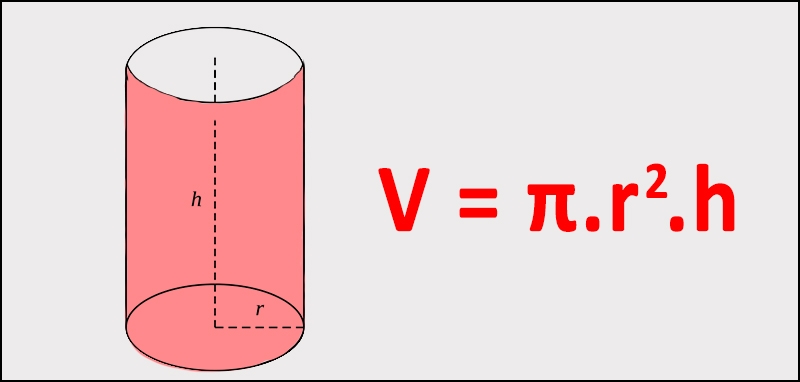
Hình trụ là một trong trong mỗi hình học tập cơ bạn dạng tuy nhiên tất cả chúng ta thông thường bắt gặp vô cuộc sống và nhiều ngành công nghiệp. Một hình trụ được tạo hình Khi một phía bằng tròn xoe được kéo dãn dài đi ra bám theo một theo hướng dọc, tạo ra trở thành một cấu tạo phụ thân chiều đem nhị lòng tròn xoe và một phía mặt mày bằng. Để nắm rõ rộng lớn về những phần mềm của hình trụ, việc nắm rõ phương pháp tính thể tích của chính nó là vô nằm trong cần thiết. Thể tích của hình trụ biểu Thị Trường tuy nhiên hình trụ rung rinh lưu giữ vô không khí phụ thân chiều, được xem bằng phương pháp nhân diện tích S lòng tròn xoe với độ cao của hình trụ.

Công thức tính thể tích hình trụ không những cần thiết trong những câu hỏi học tập tuy nhiên còn tồn tại phần mềm rất rất thoáng rộng trong những nghành nghề dịch vụ không giống nhau như kiến tạo, công nghiệp và trong cả vô cuộc sống hằng ngày. Từ việc đo lường và tính toán thể tích bể chứa chấp nước, cho tới đo lường và tính toán những không khí tàng trữ vô công nghiệp, hoặc giản dị rộng lớn là ước tính dung tích của một lon nước giải khát, công thức này rất có thể được dùng ở nhiều trường hợp không giống nhau.
Công thức tính thể tích hình trụ
Công thức
V=π×r2 ×h
Trong đó:
- V: Thể tích của hình trụ.
- r: Bán kính lòng của hình trụ.
- h: Chiều cao của hình trụ.
- π: Là một hằng số toán học tập có mức giá trị xấp xỉ vì thế 3,14159.
Ví dụ minh họa
Giả sử tất cả chúng ta mang trong mình một hình trụ với nửa đường kính lòng là 5 centimet và độ cao là 10 centimet. Chúng tớ tiếp tục vận dụng công thức tính thể tích hình trụ nhằm mò mẫm thể tích của hình này.
Bước 1: Xác quyết định những độ quý hiếm quan trọng.
- Bán kính r=5 centimet.
- Chiều cao h=10 centimet.
- Số pi (π) là 3,14159.
Bước 2: kề dụng công thức
- V=π×r2 ×h.
- V=3,14159×52 ×10.
- V=785,3975 cm3.
Vậy thể tích của hình trụ này là 785,4 cm³.

Ứng dụng thực tiễn của công thức tính thể tích hình trụ
Công thức tính thể tích hình trụ đem thật nhiều phần mềm thực tiễn vô cuộc sống đời thường, quan trọng đặc biệt trong những ngành công nghiệp và kiến tạo. Dưới đấy là một trong những ví dụ điển hình:
- Trong xây dựng: Các kỹ sư hay được sử dụng công thức tính thể tích hình trụ nhằm xác lập thể tích của những trụ cột, ống dẫn nước, và những cấu tạo hình trụ không giống trong những dự án công trình kiến tạo.
- Trong phát hành công nghiệp: phần lớn thành phầm vô công nghiệp như bể chứa chấp, thùng nhiên liệu, và thùng phuy đem hình hình dạng trụ. Tính toán thể tích của bọn chúng chung đáp ứng tối ưu hóa việc dùng không khí và nguyên vật liệu.
- Trong cuộc sống sản phẩm ngày: Khi đo lường và tính toán thể tích của những đồ dùng hình trụ tuy nhiên tất cả chúng ta dùng hằng ngày, như lon nước ngọt, chai lọ, hoặc thùng chứa chấp, công thức này trở thành khôn cùng hữu ích.
- Trong khoa học tập và nghiên cứu: Công thức tính thể tích hình trụ được dùng trong những thực nghiệm vật lý cơ và chất hóa học nhằm tính thể tích của những vật tư hoặc hóa học lỏng quan trọng.

Các sai lầm không mong muốn thông thường bắt gặp Khi tính thể tích hình trụ
Mặc mặc dù công thức tính thể tích hình trụ là một trong trong mỗi công thức khá cơ bạn dạng vô toán học tập, tuy nhiên thực tiễn Khi vận dụng vô những câu hỏi thực tiễn, nhiều người vẫn dễ dàng phạm phải những sai lầm không mong muốn kéo đến sản phẩm sai nghiêng. Dưới đấy là một trong những sai lầm không mong muốn thông thường bắt gặp Khi tính thể tích hình trụ tuy nhiên bạn phải cảnh báo.
Nhầm lộn đằm thắm độ cao (h) và nửa đường kính lòng (r)
Đây có lẽ rằng là lỗi thông dụng nhất lúc đo lường và tính toán thể tích hình trụ, nhất là so với những người dân mới nhất thích nghi với hình học tập không khí. Chiều cao và nửa đường kính đều là những thông số kỹ thuật cần thiết vô công thức tính thể tích, tuy nhiên nếu như khách hàng lầm lẫn đằm thắm nhị đại lượng này, sản phẩm sẽ ảnh hưởng sai nghiêng nguy hiểm.
Trong công thức tính thể tích hình trụ, nửa đường kính (r) là khoảng cách kể từ tâm của lòng trụ cho tới cạnh ngoài, trong những lúc độ cao (h) là khoảng cách đằm thắm nhị mặt mày lòng. Nếu lầm lẫn đằm thắm độ cao và nửa đường kính, sản phẩm đo lường và tính toán sẽ không còn đúng chuẩn vì thế diện tích S lòng tùy thuộc vào r2, còn thể tích được xác lập dựa vào nhân với độ cao.

Không tính đúng chuẩn độ quý hiếm của số pi (π)
Một trong mỗi nguyên tố cần thiết Khi đo lường và tính toán thể tích của ngẫu nhiên hình trụ này, bao hàm hình trụ, là độ quý hiếm của số pi (π). Pi là một trong hằng số toán học tập có mức giá trị xấp xỉ vì thế 3,14159. Tuy nhiên, trong không ít tình huống, người học tập rất có thể dùng những độ quý hiếm pi ko đúng chuẩn, ví dụ như thực hiện tròn xoe vượt mức hoặc dùng những ước tính ko phù hợp.
Điều này rất có thể kéo đến sai số, nhất là Khi đo lường và tính toán thể tích với những hình trụ đem độ cao thấp rộng lớn. Nếu ko đo lường và tính toán đúng chuẩn độ quý hiếm của pi, sản phẩm sau cùng sẽ không còn đáp ứng tính đúng chuẩn.
Quên đơn vị chức năng đo
Một lỗi không giống tuy nhiên nhiều người thông thường bắt gặp nên là quên hoặc dùng ko đúng chuẩn đơn vị chức năng đo Khi tính thể tích. Thể tích được đo vì thế đơn vị chức năng lập phương (cm³, m³, vv.), tuy nhiên nếu như người đo lường và tính toán ko quy đổi trúng Một trong những đơn vị chức năng đo chiều nhiều năm, nửa đường kính, và độ cao, sản phẩm sẽ không còn phù phù hợp với đòi hỏi thực tiễn.
Ví dụ, nếu như độ cao được xem vì thế mét và nửa đường kính tính vì thế centimet, tuy nhiên ko quy đổi đơn vị chức năng trước lúc vận dụng vô công thức, sản phẩm thể tích sẽ không còn khớp với đơn vị chức năng lập phương tuy nhiên đề bài bác đòi hỏi.
Mẹo đo lường và tính toán nhanh chóng và chủ yếu xác
Để đáp ứng việc đo lường và tính toán thể tích hình trụ nhanh gọn và đúng chuẩn, người học tập nên vận dụng một trong những mẹo và cách thức sau:
Sử dụng máy tính
Sử dụng PC hoặc những phần mềm đo lường và tính toán trực tuyến tiếp tục khiến cho bạn tránh khỏi nhiều sơ sót Khi tiến hành những quy tắc tính phức tạp tương quan cho tới số pi và số nón. Như vậy quan trọng đặc biệt hữu ích khi chúng ta cần thiết tiến hành nhiều quy tắc tính với chừng đúng chuẩn cao tuy nhiên không cần thiết phải tiến hành toàn bộ quá trình tính tay. Hiện ni, nhiều dụng cụ trực tuyến còn cung ứng công dụng tính thể tích hình trụ chỉ bằng phương pháp nhập những thông số kỹ thuật như nửa đường kính và độ cao.
Làm tròn xoe sản phẩm một cơ hội phù hợp lý
Khi thực hiện những câu hỏi thực tiễn, ko nên khi này các bạn cũng cần phải sản phẩm với chừng đúng chuẩn vô cùng. Trong nhiều tình huống, bạn cũng có thể thực hiện tròn xoe sản phẩm nhằm dễ nắm bắt rộng lớn và phù phù hợp với văn cảnh câu hỏi. Tuy nhiên, bạn phải cảnh báo thực hiện tròn xoe một cơ hội phù hợp, quan trọng đặc biệt Khi đo lường và tính toán những quy tắc toán tương quan cho tới số pi (π), nhằm tách sai nghiêng quá rộng.
Chọn đơn vị chức năng đo phù hợp
Chọn trúng đơn vị chức năng đo là nguyên tố khôn cùng cần thiết Khi đo lường và tính toán thể tích hình trụ. Trước Khi chính thức đo lường và tính toán, bạn phải đảm nói rằng toàn bộ những đại lượng được đo vì thế và một đơn vị chức năng, nhất là so với độ cao và nửa đường kính. Dường như, việc dùng những đơn vị chức năng phù phù hợp với văn cảnh câu hỏi (ví dụ: dùng mét khối cho những dự án công trình kiến tạo rộng lớn, hoặc lít mang lại dung tích bể chứa chấp nước) sẽ hỗ trợ sản phẩm đo lường và tính toán trở thành thực tiễn rộng lớn.
Tạm kết
Công thức tính thể tích hình trụ là một trong kỹ năng cơ bạn dạng tuy nhiên rất rất cần thiết vô toán học tập và nhiều nghành nghề dịch vụ không giống. Nắm vững vàng công thức này tiếp tục khiến cho bạn xử lý những câu hỏi một cơ hội nhanh gọn và rất có thể phần mềm trong không ít trường hợp thực tiễn biệt như kiến tạo, công nghiệp, và cuộc sống hằng ngày.
Tại FPT Shop, các bạn sẽ nhìn thấy nhiều khuôn máy vi tính giá chỉ chất lượng tốt thích hợp mang lại học viên, SV, phù phù hợp với nhu yếu học hành và vui chơi. Đừng bỏ qua thời cơ chiếm hữu những vũ trang unique với nấc giá chỉ ưu đãi. Hãy rẽ thăm hỏi FPT Shop ngay lập tức ngày hôm nay nhằm lựa lựa chọn cho chính bản thân mình một cái máy vi tính vừa lòng và tận thưởng những công tác tặng thêm thú vị.
Xem tăng về máy vi tính giá chỉ chất lượng tốt bên trên đây:
- Máy tính xách tay
Xem thêm:
- Cách tính chu vi hình chữ nhật: Hướng dẫn công thức cụ thể và bài bác luyện vận dụng mang lại học tập sinh
- Tất tần tật về diện tích S tam giác vuông và những công thức cần thiết ko thể quên